Кривые по уравнениям

[[PTM]]

Сегодня будет небольшой рассказ как нарисовать кривую по уравнению.
Навеяно воспоминанием о курсах физики курса так второго... а также ТОЭ.
Итак вспомним уравнение пространственной кривой в параметрическом виде

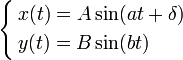
"Причем тут физика?" спросите вы.Ответ-фигуры Лиссажу.
Осцилограф припоминаете?
Для примера нам потребуется:
1.Нарисовать точку в любом месте,наиболее простое в начале координат.
2.Нарисовать прямую перпендикулярную плоскости
3.Создаем необходимые параметры
A,B,omega1,omega2,phi
где A,B- амплитуда, omega1 и omega2 частоты,phi-фаза смещения.
Для наглядности я буду использовать для частоты выражение типа
2*PI*omega*t-здесь omega число периодов колебаний.

step1.rar

(11.22 КБ) Скачиваний: 2002

4.Создаем law
x=A*sin(2*PI*omega1 *t+phi)
и
x=B*sin(2*PI*omega2)
5.Используя команду parallel curve рисуем кривые по сотворенным законам во взаимоперпендикулярных плоскостях

cu1.png (95.66 КБ) Просмотров: 76555

cu2.png (21.25 КБ) Просмотров: 76556

6.Финал используем команду combine curve

cu3.png (25.11 КБ) Просмотров: 76556

некоторые примеры
при смещении PI/2 и прочих равных- спираль
измените амплитуду одного из колебаний получите эллисную спираль.
итд.
Вот немного измененная спиралька

stepfinal.rar

(57.77 КБ) Скачиваний: 1983

Продолжение следует

[Атан]

Уважаемый [PTM], где можно посмотреть материалы по основам и практическим действиям для создания кривых по уранениям и для работы с ними в CATIA, что- то типа расширенного хелпа (чтобы меньше задавать глупых вопросов)? На русском языке.
Если вопрос бестактный, извините.

[ExtraRight]

Жень, что же ты не приложил модельку в состоянии, когда получается вот этот вот интересный случай
кривая Лиссажу

модельку в нужном состоянии прикладываю

[[PTM]]

обведите проекцию прямоугольником и посчитайте количество касаний и получите значения omega1 и omega 2, в данном случае 8 к 6 или 4/3
и вообще это подразумевалось сделать самим;)
С тебя спираль с переменным радиусом и шагом по аналогичной спирали)
Лабораторная работа
в ней есть некоторые примеры кривых

[[PTM]]

Замечу,что для уравнения заданного в явном виде достаточно первых 5 пунктов.
Одно плохо( или хорошо) какой-бы мы опорный отрезок бы не нарисовали, его длина для для parallel curve всегда
будет равна абсолютной единице.

[[PTM]]

Атан,конкретные вопросы задавайте тут.

[Атан]

Атан,конкретные вопросы задавайте тут.

Каково практическое применение кривых по уравнениям?
В каком модуле с ними работать? Ваш файл ("stepfinal") открылся в модуле "Проектирование деталей".

[[PTM]]

Атан,конкретные вопросы задавайте тут.

Каково практическое применение кривых по уравнениям?
В каком модуле с ними работать? Ваш файл ("stepfinal") открылся в модуле "Проектирование деталей".

Например, трехмерная ловушка гиперболоидного масс-спектрометра представляет собой поверхность вращения гиперболы заданной уравнением.
Времяпролетного квадрупольного фильтра масс-"extrude" гиперболы.
К тому-же построить гиперболу по аналитически полученным параметрам в скетчере "та еще задачка"
Если сложно то профили NACA тоже по уравнению строить можно.
Если совсем сложно вспомните эвольвенту;)
Открылся он в последнем, в каком вы работали.

[Zaratustra V]

А если можно, покажите пример с эвольвентой, попытался ее построить не получилось.

[ExtraRight]

А если можно, покажите пример с эвольвентой, попытался ее построить не получилось.

Я эвольвенту когда-то строил как трассу точки при кименатическом анализе - причём задаёшь параметры, получаешь кривую трассы - т.е. эвольвенту, правда уже непараметрическую

[zerganalizer]

А параллельная кривая от дуги с переменным отступом по линейному закону от нуля до N - не оно получится?

[ExtraRight]

А параллельная кривая от дуги с переменным отступом по линейному закону от нуля до N - не оно получится?

Полагаю, что нет, так как для эвольвенты расстояние мерится по касательной к дуге, а в параллельной кривой - по нормали

[Zaratustra V]

Всем спасибо эвольвенту построил, нужно было немного с направлениями подкрутить и спроецировать на плоскость.

[m-shok]

А поверхности по уравнениям кто-нибудь умеет строить?

[[PTM]]

если очень захотеть,то можно

[[PTM]]

спиральки
имеем
X=0.1*exp(0.1*1800*PI*t/100)*cos( 1800*PI*t/100)
Y=0.1*exp(0.1*1800*PI*t/100)*sin(1800*PI*t/100),
где t=0..1
и результат
в плоском виде

3.png (15.04 КБ) Просмотров: 76320

или объемном

4.png (10.63 КБ) Просмотров: 76320

и файлик

spiral.rar

(83.59 КБ) Скачиваний: 1933

на ф-цию масштаба не обращайте внимания просто у меня все маленькое и круглое становится квадратным;)

[Pacifist]

А скажите пожалуйста, как посмотреть на сам закон то... В моделях нет его:( у меня не отображает или я чего-то не понимаю... Ну тоесть в паралельной курве я вижу что используется такой то закон, а в дереве его нету..

[egorparkhaev]

подскажите а можно ли построить профиль крыла по уравнениям?

[[PTM]]

нет ничего не возможного

[noa]

Ребят, помогите. Что-то никак не могу понять, как мне построить коническую спираль с переменным шагом. Шаг задается не законом, а расстоянием от начальной точки и углом (массив данных). Конус 4 градуса. Что-то никак не могу догнать.

[racer]

Проще всего нарисовать на развёртке конуса плоскую кривую,потом накрутить плоскую кривую на конус Develop.Хотя может быть развертки конуса и не надо.

[[PTM]]

Итак вторая часть:
нам надо построить суперэллипс.
смотрим уравнение:

огонь.
добавим z(t).
и воспользуемся кнопкой .
добавляем 3 "law"

Код: Выделить всё

c:law

и прописываем в каждый из них

Код: Выделить всё

/*Law created by [PTM]*/
x=a*(((cos(0.5*PI*t*1rad))**(2/n)))*1mm

Код: Выделить всё

/*Law created by [PTM]*/
y=b*(((sin(0.5*PI*t*1rad))**(2/n)))*1mm

Код: Выделить всё

/*Law created by [PTM]*/
z=t*1mm*0


где а,b,n - обычные параметры.
Итого получаем:

Код: Выделить всё

a=b=любое число в масштабе,например 60
n=0.5

n=1.5

и мой самый любимый- иконка из ios максимально приближенная

Код: Выделить всё

a=60
b=60
n=4

при

Код: Выделить всё

n=1

получается квадрат

ну как-то так.... многого не написал, но и вы не новички